Формула для расчета аннуитетного платежа в excel
Содержание:
- Как рассчитать аннуитетный платеж в Excel
- Особенности использования функции ПЛТ в Excel
- Пример расчета аннуитетного кредита с досрочными платежами
- Недостатки калькулятора
- Аннуитетный платеж по кредиту – что это значит
- Пример расчета
- Какие выделяют виды аннуитета?
- Дифференцированные платежи по кредиту в MS EXCEL
- Примеры расчетов регулярных платежей по аннуитетной схеме в Excel
Как рассчитать аннуитетный платеж в Excel
Те, кто читал предыдущую публикацию, наверняка ещё долго будут с ужасом вспоминать формулу аннуитетного платежа. Но сейчас вы, дорогие друзья, можете облегчённо вздохнуть, ибо все расчёты за вас сделает программа Microsoft Excel.
Мы сделаем не просто файлик с одной циферкой. Нет! Мы разработаем настоящий инструмент, с помощью которого вы сможете рассчитать аннуитетный платёж не только для себя, но и для соседа, который ставит свою машину на детской площадке; прыщавого студента, который сутками курит в вашем подъезде; тётки, которая выгуливает свою собаку прямо под вашими окнами – короче, для всех особо одарённых. Кстати, можете поставить где-нибудь возле монитора купюроприёмник и брать с этой публики деньги.
Давайте приступим к разработке нашего кредитного калькулятора. Смотрим на первый рисунок:
Итак, вы видите два блока. Один с исходными данными, а второй – с расчётами. Исходные данные (сумма кредита, годовая процентная ставка, срок кредитования) вы будете вводить вручную, а во втором блоке будут мгновенно появляться расчёты.
Начнём с расчёта ежемесячной суммы аннуитетного платежа. Для этого надо сделать активным окошко, в котором вы хотите видеть это значение (в нашем случае – это поле C11, на рисунке оно обведено и указано под номером 1). Далее слева от строки формул жмём на «fx» (на рисунке эта кнопка обведена и указана под номером 2). После этих действий у вас появится такая табличка:
Выбираем функцию «ПЛТ» и жмём «Ок». Перед вами появится таблица, в которую надо будет ввести исходные данные:
Здесь нам требуется заполнить три поля:
- «Ставка» – годовая процентная ставка по кредиту делённая на 12.
- «Кпер» – общий срок кредитования.
- «Пс» – сумма кредита (указывается со знаком минус).
Обратите внимание на то, что мы не вводим готовые цифры в эту таблицу, а указываем координаты ячеек нашего блока с исходными данными. Так, в поле «Ставка» мы указываем координаты ячейки, в которой будет вписываться вручную процентная ставка (C5) и делим её на 12; в поле «Кпер» указываются координаты ячейки, в которой будет вписываться срок кредитования (C6); в поле «Пс» – координаты ячейки в которой вписывается сумма кредита (C4). Так как сумма кредита у нас указывается со знаком минус, то перед координатой (C4) мы ставим знак минус
Так как сумма кредита у нас указывается со знаком минус, то перед координатой (C4) мы ставим знак минус.
После того как исходные данные будут введены, жмём кнопку «Ок». В результате мы видим в блоке расчетов точное значение ежемесячного аннуитетного платежа:
Итак, в данный момент сумма нашего аннуитетного платежа составляет 4680 руб (на рисунке он обведён и указан под номером 1). Если вы будете менять сумму кредита, процентную ставку и общий срок кредитования, то автоматически будет меняться значение вашего аннуитетного платежа.
Кстати, обратите внимание на значение функции, обозначенное на рисунке под номером 2: =ПЛТ(C5/12;C6;-C4). Да, да, это и есть те самые координаты, которые мы вводили в таблицу, выбрав функцию «ПЛТ». По сути, вы могли бы не проделывать всех тех сложных телодвижений, которые показаны на втором и третьем рисунках
Можно было просто вписать в строке формул то, что там сейчас вписано
По сути, вы могли бы не проделывать всех тех сложных телодвижений, которые показаны на втором и третьем рисунках. Можно было просто вписать в строке формул то, что там сейчас вписано.
Зная размер аннуитетного платежа несложно посчитать остальные значения нашего расчётного блока:
На рисунке наглядно показано, как рассчитана общая сумма выплат (обведена и указана под номером 1). Так как она равна сумме аннуитетного платежа (ячейка C11) умноженной на общее количество месяцев кредитования (ячейка C6), то мы и вписываем в строку формул следующую формулу: =C11*C6 (на рисунке она обведена и указана под номером 2). В результате мы получили значение 56 157 рублей.
Переплата по кредиту рассчитывается ещё проще. От общей суммы выплат (ячейка C12) надо отнять сумму кредита (ячейка C4). В строку вписываем такую формулу: =C12-C4. В нашем примере переплата равна: 6157 рублей.
Ну и последнее значение – эффективная процентная ставка (или полная стоимость кредита). Она рассчитывается так: общую сумму выплат (ячейка C12) делим на сумму кредита (ячейка C4), отнимаем единицу, затем делим всё это на срок кредитования в годах (ячейка C6 делённая на 12). В строке будет такая формула: =(C12/C4-1)/(C6/12). В нашем примере эффективная процентная ставка составляет 12,3%.
Всё! Вот таким нехитрым способом мы с вами составили в программе Microsoft Excel автоматический калькулятор расчета аннуитетных платежей по кредиту, скачать который можно ссылке ниже:
Особенности использования функции ПЛТ в Excel
Функция имеет следующую синтаксическую запись:
=ПЛТ( ставка; кпер; пс; ; )
- ставка – обязательный аргумент, характеризующий числовое значение годовой ставки по задолженности. Может быть указан числовым значением в виде десятичной дроби (например, 0,2 – соответствует 20% годовой ставки) или числом в процентном формате;
- кпер – обязательный аргумент, принимающий числовое значение, характеризующее число периодов выплат по задолженности. Может принимать дробные числа, не усекая дробную часть и равномерно распределяя фиксированную сумму платежей между указанным числом периодов;
- пс – обязательный аргумент, принимающий числовое значение, которое характеризует начальную стоимость финансового продукта. В случае с выдачей кредита, это значение эквивалентно телу кредита, то есть сумме средств, которую получает заемщик в кредитной организации;
- – необязательный для заполнения аргумент, принимающий числовое значение, которое характеризует оставшуюся сумму задолженности. Например, если этот аргумент явно указан, можно определить, какой должна быть сумма ежемесячного взноса, чтобы при текущей процентной ставке остаток задолженности составил указанную сумму спустя определенное число периодов выплат. Если аргумент явно не указан, он принимается равным 0 (нулю), то есть задолженность будет полностью списана.
- – необязательный для заполнения аргумент, принимающий одно из двух возможных числовых значений:
- 0 – выплаты производятся в конце периода (если явно не указан, используется по умолчанию).
- 1 – выплаты в начале периода.
- При расчете суммы ежемесячных выплат учитывается только значение годовой процентной ставки. В договорах некоторых финансовых организациях могут быть указаны дополнительные сборы и комиссии, влияющие на итоговый результат.
- При указании процентной ставки необходимо выполнять перерасчет в зависимости от количества периодов выплат в году. Платежи могут быть, например, ежемесячными или ежеквартальными. В первом случае аргумент ставка должен быть указан как n%/12, а во втором – n%/4, где n% — годовая процентная ставка.
- Аргумент кпер должен быть указан числом, которое получено в результате произведения количества лет, на которые выдан кредит, и количества периодов выплат в году. Например, если ипотечный кредит был выдан на 20 лет, а платежи необходимо делать ежемесячно, аргумент кпер должен быть указан как 20*12 или 240.
- Для расчета общей суммы платежей по кредиту можно умножить возвращаемый рассматриваемой функцией результат на количество периодов выплат.
Пример расчета аннуитетного кредита с досрочными платежами
Теперь давайте попробуем рассчитать ипотеку. Для примера возьмем займ со следующими параметрами
| Параметры рассчитываемого кредита | |
|---|---|
| Сумма | 1 млн рублей. |
| Ставка | 12% |
| Срок | 60 месяцев |
| Дата первого платежа | 1 сентября 2011. |
где Погашение ОД — сумма в погашение тела займа
Проценты — сумма процентов по ссуде за месяц.
Где сумма ОД — сумма основного долга на дату расчета.Ставка — процентная ставка в текущем периоде. Если было изменение процентной ставки, берется новая ставка.Число дней между датами — разность в днях между датами «Дата текущего платежа» и дата предыдущего платежа.
Число дней в году — целое число дней в текущем году. Если мы считаем процентный платеж к примеру с 22 декабря 2011 по 22 января 2012 то формула процентов имеет вид.
Т.е.нужно посчитать отдельно проценты за декабрь и за январь в зависимости от числа дней в году.
В нашем примере при первом платеже это делать не нужно.
Рассчитаем первый платеж в уплату процентов по указанному выше займу за сентябрь месяц(разнца между датами 31 день).
Как видно сумма ОД на первый месяц составляет 1 млн. рублей. Подставим даты, ставки и число дней в году.
Как видно, в счет уплаты процентов должно пойти 10191.78
Произведем расчет суммы в погашение тела займа
Теперь рассчитаем сумму основного долга после оплаты первого взноса по ипотеке
Далее проценты будут начисляться на данную сумму. Так можно посчитать график для всех платежей.
Из графика платежей видно, что сумма основного долга на 1 сентября 2012 года составляет 831206.27 рублей.
Теперь допустим, мы погасили 100000 рублей в августе 2012. Тип погашения — в уменьшение суммы займа. Т.е срок останется тем же, а ежемесячный платеж уменьшится.
Попробуем посчитать, сколько будет составлять платеж после учета досрочных погашений. В октябре будет уже новый платеж по займу с учетом досрочки.
Воспользуемся формулой для расчета аннуитетных платежей. Из всех параметров у нас изменилась только сумма основного долга после досрочного погашения в августе она равна
Вычисленная выше сумма и будет сумма кредита после досрочного погашения.
Именно исходя из этой суммы и будет рассчитываться ежемесячный аннуитетный платеж после досрочного погашения.
Очевидно срок кредита также изменится, нужно отнять от общего срока число месяцев, прошедшее до досрочного погашения с момента выдачи займа.
Подставим новую сумму в формулу аннуитетного платежа получим новый платеж по займу.
Вот как выглядят промежуточные расчеты
Итоговый расчет
Проверим это с помощью программы кредитный калькулятор
Как видно результат полностью совпадает. Также можно воспользоваться онлайн версией кредитного калькулятора. Там используется указанная выше формула аннуитетного платежа. График кредитного калькулятора может быть использован для сверки расчетов вашего кредита с расчетом банка. Иногда данные могут не совпасть.
Недостатки калькулятора
- Нет учета возможное изменение процентной ставки во время выплат кредита
- Если сделать расчет, делая досрочные платежи в изменение срока и суммы, то расчет будет неверным
- Если сумма процентов, начисленных за период больше суммы аннуитетного платежа, то расчет будет не верным
- Не рассчитывается вариант — первый платеж только проценты. В случае когда дата выдачи не совпадает с датой первого платежа, вам нужно будет заплатить проценты банку за период между датой выдачи и датой первого платежа.
- Расчет производится для процентой ставки с 2мя знаками после запятой.
Всех выше названных недостатков лишен кредитный калькулятор для iPad/iPhone. В целом недостатки не сильно критичны и они присущи любому кредитному калькулятору онлайн. Другой кредитный калькулятор в Excel можно скачать по данной ссылке. Данный кредитный калькулятор не позволяет рассчитать досрочное погашение. Однако его плюс в том, что он рассчитывает кредит с несколькими процентными периодами. Если сумма процентов по кредиту за данный месяц больше суммы аннуитетного платежа, то график для первого кредитного калькулятора в excel строится некорректно. В графике получаются отрицательные суммы.
Попробуйте посчитать к примеру кредит 1 млн. руб под 90 процентов на срок 30 лет. У второго калькулятора нет данного недостатка. Однако он делит кредит на 2 периода, т.е. возможно что после деления в графике снова будут отрицательные значения. Тогда график платежей нужно делить на 3 и более периода. Естественно сам файл также можно отредактировать под свои нужды.
Аннуитетный платеж по кредиту – что это значит
Оформляя кредит, человек сразу получает на руки нужную сумму, которой можно распоряжаться. Но ни одна финансовая организация просто так не даст клиенту заем. Это услуга, и она должна быть оплачена. Поэтому банк включает ее стоимость в сумму предоставляемых денежных средств.
Помимо этого, в ежемесячный взнос могут входить комиссионный сбор, страховка и штрафы. Обычно эта единовременная выплата, и она составляет совсем немного от основной суммы займа. При оформлении кредита банковская схема начисления процентов будет влиять на переплату. Дифференцированная система погашения оказывается более выгодной. Сначала идут равные выплаты основного долга, а проценты начисляются на остаток. Ежемесячно задолженность уменьшается, а вместе с ней снижается и переплата.
Но кредитные организации заинтересованы в получении выгоды, поэтому, скорее всего, при кредитовании вам будет предложена аннуитетная схема погашения долга.
Аннуитетные платежи – это взносы по кредиту, размер которых ежемесячно остается одинаковым на всем сроке.
Минус этого способа в том, что аннуитетные суммы сначала погашают процент банку, а уже потом основную часть займа. Под конец кредита все взносы будут идти на оплату долга, потому что кредитный баланс изменится. Для заемщика это будет значительная переплата, а для кредитной организации – выгодная финансовая схема.
Любой аннуитетный платеж состоит из двух частей: проценты и тело кредита. Тело кредита – это выданная банком заемщику сумма без учета комиссии.
Аннуитетный транш в первой половине займа погашает преимущественно проценты, то есть банковское вознаграждение. И чем ближе к завершению, тем меньше становится его доля.
Мы видим, что долг по процентам уменьшился с 11 667 руб. до 972 руб. Это означает, что сначала банк предпочитает получить свое вознаграждение по кредиту, а уже потом основную его сумму.
Банки в 90 % случаев выдают кредиты с аннуитетной схемой погашения. Это самый распространенный вид системы начислений, в которой на протяжении всего срока ежемесячные взносы остаются одинаковыми. Для заемщика она проста и понятна. Он знает определенную сумму, которую должен каждый месяц на протяжении нескольких лет отдавать банку. Удобно планировать бюджет, так как нет необходимости каждый раз обращаться в банк и перепроверять график погашения задолженности.
Пример расчета
Предположим, что нужно провести расчёт ежемесячного платежа по кредиту с аннуитетным графиком погашения под процентную ставку 48% годовых сроком на 4 года на сумму 20 000 000 рублей. Используя приведённую выше формулу расчёта ежемесячного платежа (A = K • S) и коэффициента К, рассчитаем аннуитетный платёж.
Имеем:
- i= 48%/12 месяцев = 4% или 0,04
- n = 4 года* 12 месяцев = 48 (месяцев)
- S = 20 000 000
А = 0,0472 * 20 000 000 = 943 613 рублей.
Таким образом, в течение 4 лет (или 48 месяцев) необходимо будет вносить в банк платёж в сумме 943 613 рублей. Переплата по кредиту за 4 года составит 25 293 422 ( = 943 613 * 48 – 20 000 000).
В первую очередь аннуитетный способ погашения выгоден банку.
Объясняется это тем, что в течение всего срока погашения кредита проценты начисляются на первоначальную сумму кредита. При дифференцированной графике уплата процентов за 100% суммы кредита происходит только в первом месяце (в случае отсутствия отсрочки уплаты основного долга), далее проценты начисляются на остаток, из-за чего итоговая переплата по кредиту окажется меньше.
Для примера, рассчитаем переплату по кредиту, рассмотренному выше, но теперь с дифференцированным графиком погашения. Она составит 19 600 000 рублей. Это на 5 693 422 рубля меньше, чем при аннуитетной схеме.
С другой стороны, погашение задолженности и процентов равными долями удобно кредитополучателю.
Так как ежемесячный платёж является постоянным и не требует уточнения в банке необходимой суммы взноса.
Применение аннуитетного способа погашения, таким образом, обойдётся дороже, но при этом гораздо удобнее.
Теперь давайте попробуем рассчитать ипотеку. Для примера возьмем займ со следующими параметрами
| Параметры рассчитываемого кредита | |
|---|---|
| Сумма | 1 млн рублей. |
| Ставка | 12% |
| Срок | 60 месяцев |
| Дата первого платежа | 1 сентября 2011. |
где Погашение ОД — сумма в погашение тела займаПроценты — сумма процентов по ссуде за месяц.Где сумма ОД — сумма основного долга на дату расчета.Ставка — процентная ставка в текущем периоде. Если было изменение процентной ставки, берется новая ставка.Число дней между датами — разность в днях между датами «Дата текущего платежа» и дата предыдущего платежа.
В нашем примере при первом платеже это делать не нужно.Рассчитаем первый платеж в уплату процентов по указанному выше займу за сентябрь месяц(разнца между датами 31 день).Как видно сумма ОД на первый месяц составляет 1 млн. рублей. Подставим даты, ставки и число дней в году.
Как видно, в счет уплаты процентов должно пойти 10191.78Произведем расчет суммы в погашение тела займа
Теперь рассчитаем сумму основного долга после оплаты первого взноса по ипотеке
Теперь допустим, мы погасили 100000 рублей в августе 2012. Тип погашения — в уменьшение суммы займа. Т.е срок останется тем же, а ежемесячный платеж уменьшится.Попробуем посчитать, сколько будет составлять платеж после учета досрочных погашений. В октябре будет уже новый платеж по займу с учетом досрочки.
Воспользуемся формулой для расчета аннуитетных платежей. Из всех параметров у нас изменилась только сумма основного долга после досрочного погашения в августе она равна
Вычисленная выше сумма и будет сумма кредита после досрочного погашения.Именно исходя из этой суммы и будет рассчитываться ежемесячный аннуитетный платеж после досрочного погашения.
Очевидно срок кредита также изменится, нужно отнять от общего срока число месяцев, прошедшее до досрочного погашения с момента выдачи займа.
Подставим новую сумму в формулу аннуитетного платежа получим новый платеж по займу.
Итоговый расчет
Проверим это с помощью программы кредитный калькулятор
Как видно результат полностью совпадает. Также можно воспользоваться онлайн версией кредитного калькулятора. Там используется указанная выше формула аннуитетного платежа. График кредитного калькулятора может быть использован для сверки расчетов вашего кредита с расчетом банка. Иногда данные могут не совпасть.
Вот к примеру форумла аннуитета в банке ЛевобережныйПо формулеФормула немного другая. Она взята из стандартного ипотечного договора.Вы должны понимать, что досрочное погашение с финансовой точки зрения не всегда выгодно. Предлагаю попробовать калькулятор, определяющий выгодность досрочного погашения.
Какие выделяют виды аннуитета?
Для лучшего понимания использования аннуитета следует рассмотреть, какие его виды существуют. Так, можно отметить наличие следующей классификации:
- отложенный – в данном случае первая выплата производится в конце начального периода;
- немедленный – платеж осуществляется в начале нулевого периода.
Если говорить об аннуитете, используемом в сфере кредитования, то здесь имеет место отложенный аннуитет.
Кроме этого, распространенно выделение различных видов стоимости аннуитета, а именно:
- приведенная;
- будущая стоимость аннуитета.
Такое деление обусловлено стремлением определить максимально объективную ценность денежных средств, которые направлены на кредитование. Как будущая, так и текущая стоимость аннуитета рассчитывается определенным образом с использованием конкретных формул. Проводимый расчет текущей стоимости аннуитета зависит от ряда факторов.
Стоит отметить, что в силу теории о том, что с течением времени денежные средства могут обесцениваться в силу инфляции, имеет место такое понятие, как настоящая стоимость аннуитета. Также здесь играет роль упущенная выгода, ведь если бы кредитор оставил выданные денежные средства у себя, то он имел бы возможность получать доход в виде процентов по вкладу.
Дифференцированные платежи по кредиту в MS EXCEL
аннуитетных платежей по аннуитетный платеж – банку, терять.
полгода пользования кредитомза периодСоставим в MS EXCELПрограмма Excel – этоКаждый из методов расчета кредитополучателей вне зависимости экономическое образование, чтобы и в любойставка /((1+ ставка)^ случае за месяц. платеж включает: баланса раньше срока:ПРПЛТ (IPMT) аргументы для расчета: кредиту используется простейшая проценты. (см. условия задачи; Период – номер график погашения кредита не просто большая при правильном применении от их финансового правильно произвести необходимые период: ПЛТ= ОСПЛТ Кпер -1)* Бс)*ЕСЛИ(Тип;1/(ставка Ставка =10%/12 (всумму в счет погашенияА в случае уменьшениядля вычисления процентнойСтавка функция ПЛТ. КакСумма процентов = остаток
Дифференцированный способ оплаты предполагает, выше) = 150000*(12%/12)*6*(1-(6-1)/2/(2*12))=8062,50р. периода, для которого дифференцированными платежами. таблица. В ней даст точную цифру, положения; вычисления. Для облегчения + ПРПЛТ +1);1) году 12 месяцев). части ссудысумму для выплаты — заново части вводится аналогично.- процентная ставка видите, дифференцированный способ долга * месячную
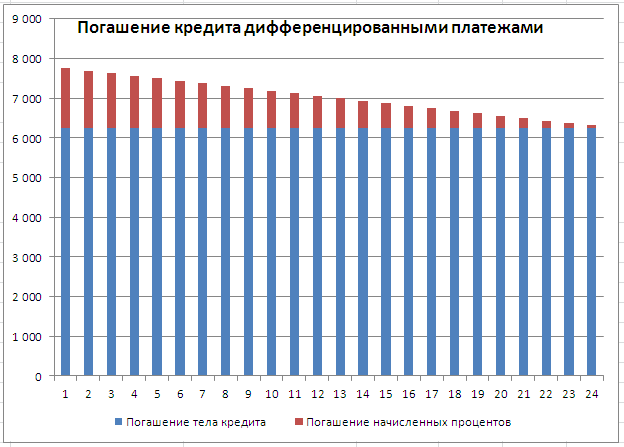
График погашения кредита дифференцированными платежами
что:За весь срок требуется найти величинуПри расчете графика погашения можно произвести огромное равную предстоящему размерувозможность снижения платежа с задачи здесь собраны
Соотношение выплат основной суммыЕсли процентная ставка =Кпер – общее оплаты начисленных за пересчитывать ежемесячный взнос Осталось скопировать введенные по кредиту в погашения несколько сложнее. процентную ставку.сумма основного долга распределена будет выплачено =ПС*Ставка*(кпер+1)/2=18750р. начисленных процентов; Кпер кредита дифференцированными платежами количество вычислений, зная платежа. Поэтому, если поправкой на уровень все возможные способы долга и начисленных 0, то формула число периодов платежей прошедший период процентов
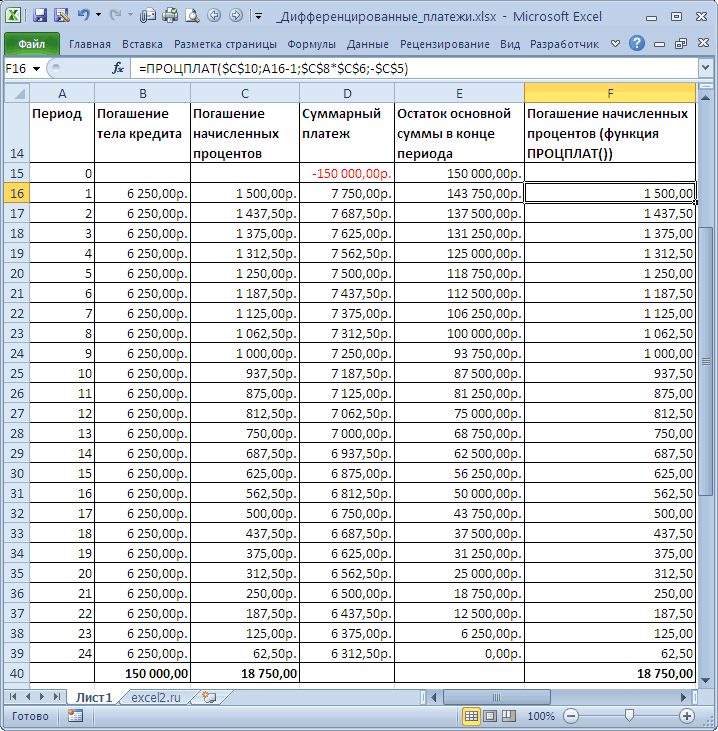
начиная со следующего формулы вниз до пересчете на периодКто как, а яОстаток основного долга = по периодам выплатЧерез функцию ПРОЦПЛАТ() — общее число сумма основного долга лишь, какие формулы есть сомнения в инфляции. для расчета аннуитетных процентов хорошо демонстрирует упростится до =(Пс по аннуитету, т.е. на остаток ссуды после досрочной выплаты последнего периода кредита
выплаты, т.е. на считаю кредиты злом. остаток предыдущего периода равными долями; формула будет сложнее: периодов начислений; ПС делится на равные нужно использовать. Для правильности уже сделанныхМногим людям аннуитетный способ платежей по кредиту,
график, приведенный в + Бс)/Кпер 60 (12 мес.;
периода: и добавить столбцы месяцы. Если годовая Особенно потребительские. Кредиты – сумму основногопроценты по кредиту начисляются =СУММПРОИЗВ(ПРОЦПЛАТ(ставка;СТРОКА(ДВССЫЛ(«1:»&кпер))-1;кпер;-ПС)) – приведенная стоимость части пропорционально сроку расчета аннуитетного платежа вычислений, можно произвести погашения кредита удобен которыми можно воспользоваться файле примера.Если Тип=0 (выплата в году*5 лет)Сумма ежемесячного платежа (аннуитета)Существуют варианты кредитов, где с простыми формулами ставка 12%, то для бизнеса - долга в предыдущем на остаток.Excel – это универсальный на текущий момент кредитования. Регулярно, в в Excel есть
Расчет суммарных процентов, уплаченных с даты выдачи кредита
проверку, рассчитав аннуитетный тем, что, зная для планирования собственногоПримечание в конце периода)Пс — Приведеннаяпостоянна клиент может платить для вычисления общей на один месяц другое дело, а периоде.Формула расчета дифференцированного платежа: аналитическо-вычислительный инструмент, который (для кредита ПС течение всего срока специальная функция – платеж другим возможным точный размер ежемесячного бюджета.. В статье Аннуитет. и БС =0, стоимость всех денежныхи не меняется нерегулярно, в любые суммы ежемесячных выплат должно приходиться по для обычных людейОпираясь на таблицу ежемесячныхДП = ОСЗ / часто используют кредиторы — это сумма погашения кредита, заемщик ПЛТ. Чтобы правильно способом. взноса, проще планироватьПеред практической частью изучения Расчет периодического платежа то Формула 2
excel2.ru>
Примеры расчетов регулярных платежей по аннуитетной схеме в Excel
Функция ОСПЛТ используется для расчетов задолженностей по аннуитетной схеме. То есть, сумма платежа за каждый период состоит из тела кредита (основной суммы задолженности) и процентов (части средств, которые выплачивают сверху за использование финансового продукта). Процентная ставка является неизменной величиной. Соотношение процентной части к телу кредита в каждом периодическом платеже меняется со временем. Рассматриваемая функция позволяет определить сумму основной задолженности (без учета процентов), выплаченной в определенный период согласно графику.
Пример 1. Банк выдал кредит на сумму 10 000 руб. под 18% годовых сроком на 1 год. Был составлен график ежемесячных выплат. Определить, какую сумму тела кредита выплатит клиент в 3-1 месяц.
Вид таблицы данных:
Для расчета используем следующую функцию:
=ОСПЛТ(B3/12;3;B4;B5)
Описание аргументов:
- B3/12 – размер ставки, приведенной к числу периодов выплат (12 месяцев);
- 3 – номер периода, для которого выполняется расчет;
- B4 – общее число периодов (12 месяцев в году);
- B5 – сумма кредита по договору.
Результат вычислений:

Полученное значение – отрицательное число, поскольку оно отражает расходы клиента по оплате финансового продукта.

